Posts

/by

Derivatives – Another Option For Helping Mitigate Interest Rate Risk

,

The Federal Reserve signaled their expectation to continue Fed Funds rate increases in 2017, but substantial uncertainty remains about when and where market rates will move.  Credit unions can find it challenging to achieve a desirable ROA today while maintaining an acceptable level of risk should market rates increase.  Decision-makers have a variety of options available for attacking interest rate risk challenges, and derivatives can be another useful arrow in the ALCO quiver.

Some of our clients are using or considering derivatives as a tool for mitigating interest rate risk.  While c. myers does not sell derivatives, we regularly model their impact on our clients’ financial structures to show the risk and reward trade-offs.

Derivatives can be thought of as purchasing insurance.  As an example, consider your purchase of an auto insurance policy.  You pay a premium to provide protection for your car from accidents, theft, etc.  The premium may be paid over the course of years.  If the car is never damaged or stolen, the insurance protection is never used or realized.  Overall of course, you’re probably happy that the insurance wasn’t needed.  Was the insurance valuable?  Was it worthwhile?

Derivatives operate similarly to protect against interest rate risk.  There are a variety of derivatives available to credit unions.  To illustrate some of the key attributes, let’s consider caps and swaps.

A cap is insurance purchased for a fixed price up front and provides protection for a specific time frame (the term) for market rates that go above a specific level (the strike rate).  Credit unions establish a notional balance, say $100 million, which never exchanges hands but is used like a principal balance for determining the interest payments.  If market rates increase to a point where they exceed the strike rate, the difference between the market rate and the strike rate is applied against the notional balance and paid to the credit union.  The cost of this insurance is largely determined based on the strike rate and term desired by the credit union, but again it is known and fixed up front.

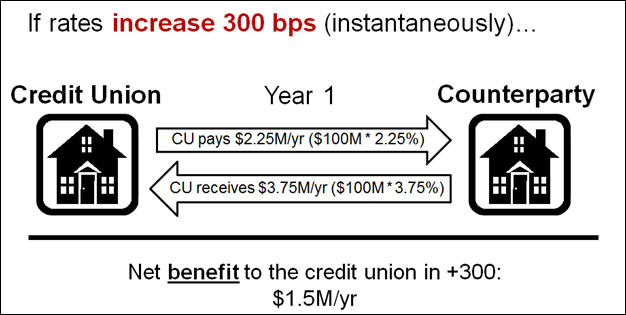
Unlike a cap, an interest rate swap is not purchased for a fixed price.  In fact, there is no up-front cost for the swap.  Rather, two parties agree to pay each other different interest rates on a given notional amount for the term of the swap.  One party will pay a fixed rate, while the other will pay a variable rate based on an index such as LIBOR.  The idea is that as market rates increase, the variable rate could at some point exceed the fixed rate payment and offer protection to the fixed rate payer.  Consider the following interest rate swap example with a notional amount of $100 million, where the credit union pays a fixed 2.25% rate and receives
1-month LIBOR.

17-02-tlb-blog-derivatives1

17-02-tlb-blog-derivatives2

In this example, for simplification, an instantaneous rate change was assumed.  However, the timing and direction of market rate changes will ultimately determine the resulting cost or benefit of the swap over its term.

Derivatives can be a valuable tool for credit unions to consider within their interest rate risk management strategy.  When deciding whether to use derivatives, it is important to understand both the expected interest rate risk protection, as well as the potential costs within a range of rate environments.  It also makes sense to ask how the protection may change over time and whether there are circumstances that might make the protection not as valuable.  For more detailed information about derivatives and understanding key considerations, please see our c. notes paper, Considering Derivatives?

/by

c. notes – Considering Derivatives?

,

Credit unions purchase derivatives for interest rate risk (IRR) protection. As we consider the value that can be obtained from derivatives, it also makes sense to ask how that protection may change over time and if there are circumstances that might make the protection not as beneficial.

Many of our clients are using or considering derivatives as a tool for mitigating interest rate risk. While c. myers does not sell derivatives, we regularly model their impact on our clients’ financial structures to show the risk and reward trade-offs. As we model and discuss these with our clients, we’ve made some observations and identified some questions that help bring a greater understanding to what a credit union might expect. We believe that introducing additional tools to help credit unions address interest rate risk is a very good thing and, as with any new tool, it’s important to understand how it can be used and what risk and reward trade-offs it offers.

To continue reading, please visit the article here.

/by

Evaluating Derivatives―Part VI: Why Use Derivatives?

,

With the derivatives rule that went into effect in 2014, NCUA gave credit unions access to a new tool to help mitigate interest rate risk. Although a derivatives pilot program has been around since 1998, derivatives are still a relatively new thing to the industry. Past blogs in this series have provided the reader with important things to consider about the cash flows and economic value of interest rate swaps. All this, and more, should be carefully evaluated if your credit union is considering derivatives.

So, with all these things to consider, why might a credit union enter into a derivatives contract? The answer is simple: to hedge interest rate risk. As with other hedging techniques, a derivative will cost something today, but will help if rates increase. Think of it like an insurance policy.

For example, let’s suppose a credit union’s ALCO has decided it would be desirable to reduce interest rate risk and has established an internal goal of remaining Well Capitalized if rates increase 500 bps, and maintaining an NEV volatility of not greater than 40%. However, as shown below, an interest rate risk simulation indicates that if rates increase 500 bps, the credit union is positioned to put net worth of 3.64% at risk, leaving 6.56% net worth remaining. In addition, net economic value volatility is 55.55% and the resulting net economic value is 6.08%.

In evaluating ways to reduce its risk, the credit union runs a what-if scenario on the following interest rate swap:

  • 7-year term
  • Notional Amount: $50 million
  • Pay Fixed Rate: 2.00%
  • Receive Floating Rate: 3-month LIBOR

The results are shown below.

An interest rate swap is expected to provide protection, or insurance, against a rising rate environment. As noted above, the cost of this insurance in terms of annual ROA is 13 bps in the current environment. The benefit shown is the improvement in long term net worth at risk. The simulation including the impact of the swap shows that:

  • Current ROA is reduced by 13 bps
  • Long-term net worth not at risk improved by 78 bps to 7.34%
  • The point at which the financial structure could now be positioned to fall below Well Capitalized has improved from when short-term rates are at 5% to when they now reach 6%

Note:  $s in 000s
Derivatives analytics provided by The Yield Book® Software.

The NEV results both with and without the impact of the derivatives are shown above. Notice that the resulting NEV ratio after layering in the derivatives has improved in the +500 shock from 6.08% to 8.24%. Similarly, NEV volatility for that rate environment has been reduced from 55.55% to 38.31%. The ALCO has achieved their desired results.

While there are many things to consider about derivatives, they can be a good tool for mitigating interest rate risk. The more analysis that is done and the better your credit union’s unique risks and risk tolerances are understood, the better equipped you will be to decide if derivatives are a good choice for your credit union.

/by

Evaluating Derivatives―Part V: Economic Value Declines Over Time

Credit unions purchase derivatives to receive value: interest rate risk protection. This blog series set out to help decision makers understand the variety of outcomes they could observe over the life of a derivative, and how those outcomes will ultimately determine the value realized.

Over its life, derivative economic value is impacted by two forces:

  • Changing rate environments – which can increase or decrease economic value
  • Time – which continuously decreases economic value gains

Prior blog articles discussed the impact of changing rate environments on economic value. Regardless of the rate environment, economic value of a derivative will converge to zero at maturity. The value of the protection diminishes as the remaining time to maturity becomes less. Using our prior example of the 7-year swap, the chart below shows the economic value on day 1 and each year thereafter:

Note:  $s in 000s
Derivatives analytics provided by The Yield Book® Software.

The chart demonstrates the economic values for the various rate shocks as the time until maturity shortens. Compare the highest shocked environment shown, +500, the initial value of $26.4 million to the year 1 shocked value of $22.8 million. The year 1 value is materially lower because the swap only offers 6 remaining years of protection. Independent of the rate environment, by the end of year 7 the swap no longer has value since it matures.

Why is this important? If the swap was originally purchased to address a volatility issue in the credit union’s financial structure and that volatility persists, then over time the credit union will need to either adjust the underlying structure or will need to purchase additional swaps to maintain the same level of protection. It can be important to be clear about the objectives of the derivatives. Is the purchase designed to offset an existing risk and buy time until the root interest rate risk can be addressed? On the other hand, is the intent to, ongoing have, a business model incorporate additional interest rate risk and perpetually utilize derivatives to offset the risk?

/by

Evaluating Derivatives―Part IV: The Relationship Between Value and Cash Flow

Our last post on derivatives explored the relationship between rate shocks and changes in value. Inherent to this was a caution that improvement in value due to changes in the implied path of interest rates doesn’t guarantee cash flows will be positive in the future.

The economic value analysis is typically limited to assuming an implied path. When performing cash flow tests (earnings), however, that limitation is not necessary or warranted. Since there are virtually an unlimited number of paths that can occur, consider paths that could expose risk. Recent history has demonstrated that the risk of rates remaining flat should not be ignored.


Forward curve analytics provided by The Yield Book® Software.

For each rate environment, communicating the potential of rates going to that level and staying there can often expose potentials that won’t be seen from the economic value. Note that in this example, while rates change instantly, the earnings lag the initial year due to the quarterly reset.


Note: $s in 000s

It can also be beneficial to understand the impact of rates changing over time. Consider the difference of a 12-month rate change.


Note: $s in 000s

Note in this example that, if rates ramp up 200 bps over 12 months and stay at that level, the credit union earnings from the derivative do not break even until the 6th year. This is in contrast to the +200 instant change showing a break even in the 3rd year.

In order to reduce the risk of being blindsided from an earnings perspective, institutions should review the earnings potential of rate shifts that hold steady at the simulated level. Institutions should also understand the potential impact of slower rate changes.

Compare this to the economic value displayed in the previous blog where there is no hurt in the current environment and there are material gains in the other environments.


Derivatives analytics provided by The Yield Book® Software.